今日はちょっと高学年向けの話になってしまうかもしれません。(低学年の人でも、算数が得意!という人はぜひ読んでね。)
図形の学習が始まると、先生たちはよ~~~~く言いますね。「図をかきなさい。」「まっすぐ線を引きなさい。」「小さくかくな。大きくかけ。」などなど。そんなとき、「うぇー」と思いつつもちゃんと直してくれる人もいれば、「えー別に良いじゃん。できるし。」などとのたまうかわいらしいあんぽんたんさんもいるわけです。まったく。僕たちが変に綺麗好きだからそんな無駄なことを言っている、とでも思っているんでしょうか。僕のどこを見て思っているんでしょうか。僕が綺麗好きなわけないじゃない。
図を整えてある程度正確にかく意義はふたつ。「まちがえないため」と「図形に強くなるため」。今回はこれを具体的な例を示してみなさんに再確認してもらおうかなと思います。
というわけで「この世のすべての三角形は実は二等辺三角形だった!?」という恐ろしい真実をお話しましょう。
まずは図1のようにタネもシカケもない三角形ABCを用意します。図2のように、辺BCのまん中の点DからBCに垂直な線と、角Aの大きさを半分にわけるような直線を引き、ぶつかった点をPとします。さらに点Pから辺AB、ACに垂線を引き、ぶつかった点をそれぞれE、Fとします。このとき、三角形AEPと三角形AFPは、図3のようにくっつけると長方形になるので合同ですから、PE=PF、AE=AFです。また、三角形PBCはPB=PCの二等辺三角形です。すると図4の三角形BPEと三角形CPEは、図5のようにくっつけると二等辺三角形になるので合同ですから、BE=CFです。ここまでをまとめると、図6のように、AE=AFで、BE=CFですから、AE+BE=AF+CF、つまり、AB=ACです。したがって何の変哲もない三角形ABCは二等辺三角形になります。言いかえると、すべての三角形は二等辺三角形である、ということになります。
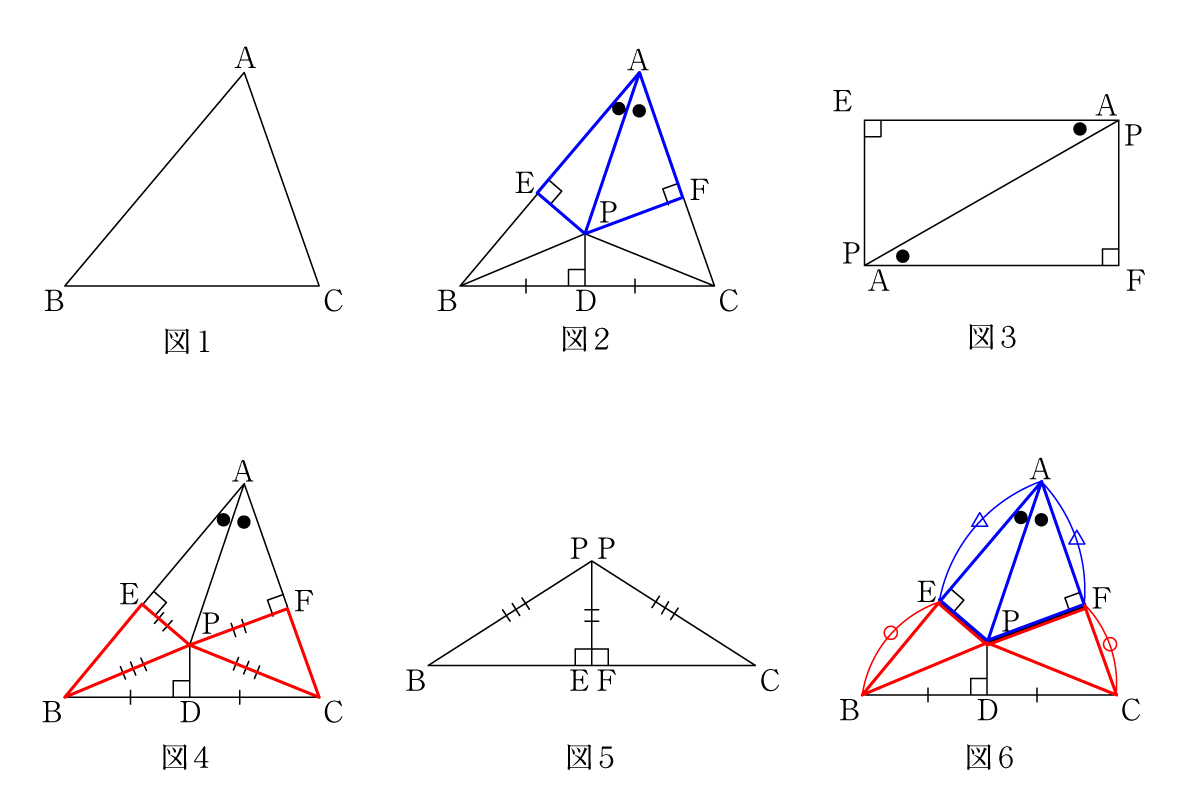
そしてもちろんそんなことがあるわけないので、この説明はもちろんどこかがおかしいのです。ここからはどこがおかしいのか、ネタばらしがありますので、「自分で考えたい!」という人は1回考えてから続きを読んでください。
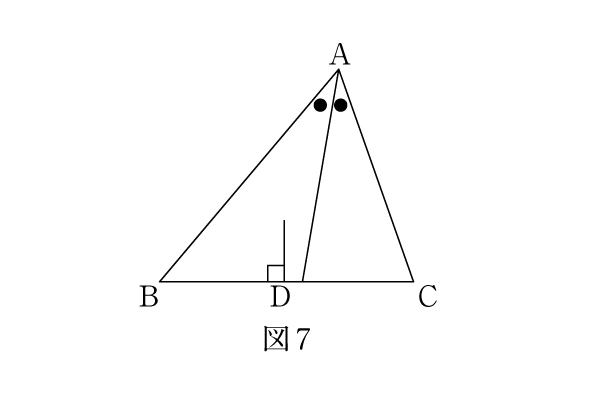
今回おかしかったのは、図2です。本当は図7のように、点Dから垂線を引くと、角Aからひいた角度を半分に分ける線は、三角形ABCの内部ではぶつからないのです。だから、「図がまちがっている」ということなんですね。いざというときに正しい図がかけないと、こんなとんでもないミスにつながってしまう、ということです。
さらに、ふだんから自分である程度正確に図をかき続けている人は、長さや角度の感覚が鋭くなっていきます。そういう人は、「実はこの部分にこんな図形が隠れているんじゃないか」というように問題を解く上でポイントとなる図を見つけやすいのですね。今回の例であれば、直線APで分けたふたつの角度が全く等しくないことにすぐに気づいたかもしれません。ですから、それなりに整った図をかくことそのものが図形の問題を解く力を育むのです。というわけで、図をかく習慣もナシに「図形ができません。」などというのは図々しいのです。図だけに。

