「確率」の話をしましょう。数ヶ月前ののぞみ通信でも確率について少し触れていますが、今回は確率について考えることが主目的です。算数ではあまり扱われる機会のない学問ですが、数学では1つの大きな単元として取り上げられます。今のうちに触れておいて損はないでしょう。友達とのゲームに勝つ確率もあがるかもしれませんよ!
まずは基礎的な内容から。例えば「コインを1枚投げて表が出る確率」は1/2(2分の1。のぞみ通信内ではこの表記で我慢してください!)。「さいころを1回投げて1が出る確率」は1/6。なんとなくわかりますね。では「コインとさいころを1つずつ投げて、コインは表、さいころは1が出る確率」はいくつでしょうか。イメージとしては次の図のようになります。
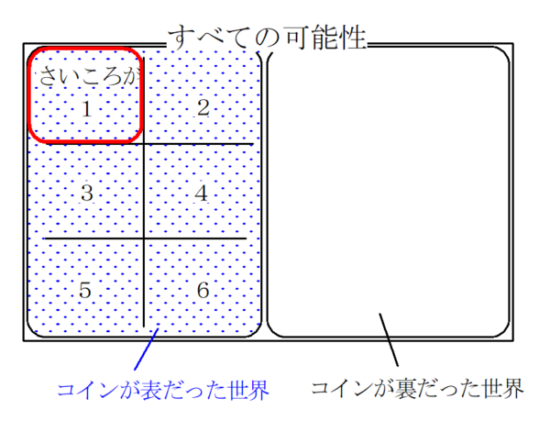
あなたがコインを投げることで、1/2は「コインが表だった世界」につれていかれ、残りの1/2は「コインが裏だった世界」につれていかれます。それぞれの世界の1/6でさいころの目が1ですので、コインやさいころをなげる前の状態から、1/2 × 1/6 = 1/12の確率で「コインが表、さいころが1」の世界につれていかれる、というわけです。(もちろんどんなときでも簡単にかけ算で確率を計算できるわけではありませんが、今回のところはややこしい話をぬきにしちゃいます。)
ちょっとずつ応用していきましょう。先ほど確認したように、「コインを1枚投げて表が出る確率」は1/2で、もちろん逆の「コインを1枚投げて裏が出る確率」も1/2です。さらにかけ算を使うことによって、「コインを2回連続で投げて、両方とも表が出る確率」は1/2 × 1/2 = 1/4 となります。では「コインを2回連続で投げて、少なくとも1回は裏が出る確率」はどう計算できるでしょうか。場合の数の学習で「余事象」を習っている人は簡単ですね。「少なくとも1回は裏」というのは「2回とも表だったとき以外」のことです。つまり先ほどの例で使った図と同じようなものを考えると図2のようになるわけです。
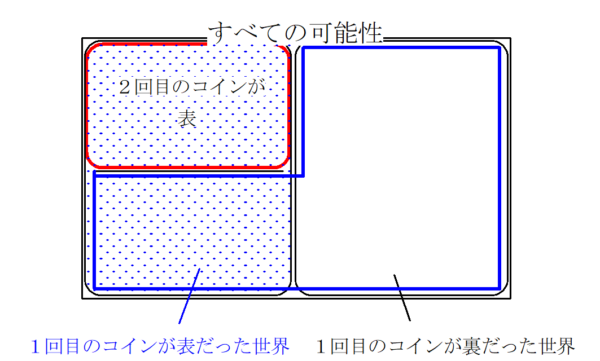
全体を1として考えているので、求める確率(図2の青枠の部分)は1- 1/4 = 3/4 で計算できるのですね。では練習です。「さいころを3回投げて少なくとも1回は2以下の目が出る確率」はいくつでしょうか。「さいころを1回投げて2以下の目が出る確率」は2/6=1/3です。ということは逆に「さいころを1回投げて3以上の目が出る確率」は1- 1/3 = 2/3ですね。先ほどと同じように計算すると、1- 2/3 × 2/3 × 2/3 = 19/27となります。
では最後の問題です。「袋の中に100個のうち1個だけあたりが入ったくじがある。このくじは1回引いてあたりかはずれかを確認したら引いたくじを袋に戻し、つぎにくじを引くときはまた100個のくじから1個を引く。このくじを100回引いて少なくとも1回あたりを引く確率を求めなさい。」
計算部分はあまりに大変なのでコンピュータに任せて、式までを考えていきましょう。
「1回くじをひいて当たる確率」はもちろん1/100。「1回くじをひいてはずれる確率」は1- 1/100 = 99/100です。「少なくとも1回あたり」というのは「全部はずれだったとき以外」ということになりますから、次のように計算できますね。1- 99/100 × 99/100 ×……× 99/100 × 99/100 (99/100を100回かける) これをコンピュータに計算してもらいました。その結果、0.63396……となり、およそ60%ちょっとだとわかります。式の立て方なんかは難しくないですね。ただしとても手計算できるものではないので入学試験では出ないでしょう。今回みなさんに知っておいてほしいのはこの結果です。「100回くじをひいて少なくとも1回あたりをひく確率はおよそ60%」ということですがいかがでしょうか。「100回も引けるなら1回くらいひけるだろ!」という感覚はけっこう危険じゃないですか? 60%ということはそれこそ「トランプの1~10の10枚から1枚引いて、6以下を引く確率」などと置き換えることができます。ぜひ何回かトランプを引いてみてください。60%って半分を越えているから希望をもちやすいけど、思った以上に裏切られる確率です(これは完全に私の主観ですね)。
このように日常のちょっとした確率を計算するの、なかなかおもしろいですよね。でも勘違いしちゃいけないのは、あくまで紙の上の計算だということ。実際に60%という確率が「5回に3回絶対にそうなる」というわけではないのは1/100のくじの話で計算した通りです。確率を計算するのは楽しいけれどそれに踊らされてもいけません。「確率を計算したら90%もある。楽勝!」ってそれ、小説だったら死亡フラグですよ。

